My Final Word on Spines

TECH NOTE 35: All shafts have certain characteristic. One is that they all have 180-degree symmetry. That is, if it takes a given force to bend a shaft one inch in a given direction it will take the same force to bend it an inch in the opposite direction. There is no such thing as a "hard side" or "soft side" when it comes to a shaft. There is always 180-degree symmetry even if the cross sectional shape of the shaft looks like an amoeba! Every shaft has a strongest and a weakest plane. In the mechanical engineering textbooks they are called the principal and the neutral planes. Clubmakers tend to call them the S1/S2 plane and the N1/N2 plane. They are always 90 degrees apart. Once again they represent a plane through the shaft Just a side note, the N and S planes of the shaft are its natural frequency planes. A shaft vibrating in either of these planes will not wobble. It will vibrate in a straight like called "flat lie oscillation" or FLO. Twanged anywhere else and both natural frequencies will be excited and the shaft will wobble in various oval patterns.

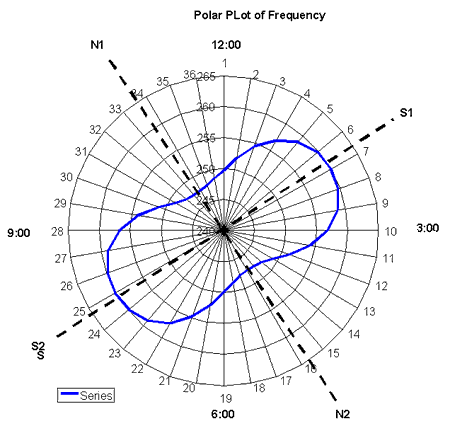
An X-Y plot of a typical shaft with a large variation in frequency was shown in Tech Note 13 "Spines vs. Frequency". It always looks like a sine wave which makes two complete cycles in 360 degrees. In trying to explain the characteristics of a shaft and how it might best be aligned in the club this was probably not the best was to depict the data. Rather than plot the frequency data in an X-Y format a polar plot would have been much more informative. In a polar plot the angles 0 through 360 degrees are shown as the face of a clock. Zero being at 12:00, 90 degrees being at 3:00 etc. The frequency data are shown as the distance from the center of the clock to its outside edge. Let's say the center is 240cpm and the outside edge of the clock is 265cpm. A typical shaft with a large frequency variation is plotted in this polar in the Figure below.

A polar plot is as if you're looking right down the cross section of the shaft. Where it's diameter is thickest it's the stiffest, that is, having the highest frequency and of course where it's thin it would be the weakest. Think of a yardstick.. These are the strong and weak planes of the shaft and have been labeled the S1-S2 and the N1-N2 planes. The 90 degree relationship between the two as well as the 180 degree symmetry are quite obvious when the data are shown in this format. The shaft's logo was at 12:00 in this example.

Now the question arises how would it be best to align this shaft in a golf club. For visualization purposes think of 12:00 being the position of the ball as you address it. 9:00 is the direction of the green, 6:00 is the direction of your feet and 3:00 is away from the target. Assume the logo on the shaft is pointed at 12:00. Let's also assume that in the hitting area the major forces on the shaft are trying to bend it in the 9:00 - 3:00 plane. This is probably not precisely the case especially with the variation in swings from golfer to golfer but it's not an unreasonable assumption. To figure out how best to align the shaft let's try a little mind experiment. Make a cardboard cutout of the cam like shape in the attached Figure and stick it right on top of Figure with a thumbtack. The cut out now overlays the actual cam shape. Now lay a paddle-pop stick flat on the plot say at 12:00 and slide it down in the direction of 6:00 until it hits the card board cutout. Which way will the cutout rotate? Clockwise. Now try say 2:00. Again clockwise but much more vigorously. Where will the cutoff stop rotating? When the N1-N2 axis is aligned with the paddle pop stick. In other words a force applied along the N axis will cause no rotation of the shaft. What if the stick is pressed along the S1-S2 axis? It will again be stable but in this case it will be conditionally stable. If the force gets slightly out of the S plane the cutout will immediately flip to the N plane.

So if this were my club where would I align the shaft? I'd put the N1-N2 plane at 9:00 - 3:00 and my logo would now be pointing at about 10:00 rather than 12:00. I'd of course have to explain to the customer that I was not drunk when I installed the shaft!